Source: Steve Zylius / UCI
News • Fractional exponents
New approach for more accurate epidemic modeling
A new class of epidemiological models based on alternative thinking about how contagions propagate, particularly in the early phases of a pandemic, provide a blueprint for more accurate epidemic modeling and improved disease spread predictions and responses, according to a study by researchers at the University of California, Irvine and other institutions.
In the paper published in Scientific Reports , the scientists said that standard epidemic models incorrectly assume that the rate in which an infectious disease spreads depends on a simple product of the number of infected and susceptible people. The authors instead suggest that transmission happens not through complete mingling of entire populations but at the boundary of sub-groups of infected individuals.
“Standard epidemiological models rely on the presumption of strong mixing between infected and non-infected individuals, with widespread contact between members of those groups,” said co-author Tryphon Georgiou, UCI Distinguished Professor of mechanical and aerospace engineering. “We stress, rather, that transmission occurs in geographically concentrated cells. Therefore, in our view, the use of fractional exponents helps us more accurately predict rates of infection and disease spread.”
The researchers proposed a “fractional power alternative” to customary models that takes into account susceptible, infected and recovered populations. The value of the exponents in these fractional (fSIR) models depends on factors such as the nature and extent of contact between infected and healthy sub-populations.
The authors explained that during the initial phase of an epidemic, infection proceeds outwards from contagion carriers to the general population. Since the number of susceptible people is much larger than that of the infected, the boundary of infected cells scales at a fractional power of less than one of the area of the cells.
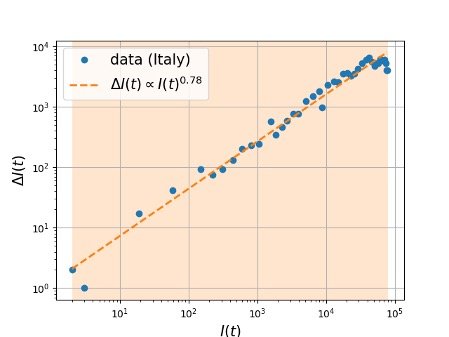
The researchers tested their theory through a series of numerical simulations. They also fitted their fractional models to actual data from Johns Hopkins University Center for Systems Science and Engineering. Those data covered the first few months of the COVID-19 pandemic in Italy, Germany, France and Spain. Through both processes they found the exponent to be in the range of .6 and .8.
When presented on a graph, data from Johns Hopkins University of infection rates in Italy during the first few months of the COVID-19 pandemic show the change in the number of infected individuals and subsequent growth of the epidemic. This trajectory matches a fractional power of the infected sub-population at different times during the epidemic progression.
“The fractional exponent impacts in substantially different ways how the epidemic progresses during early and later phases, and as a result, identifying the correct exponent extends the duration over which reliable predictions can be made as compared to previous models,” Georgiou said.
In the context of the current COVID-19 pandemic, better knowledge about propagation of infections could aid in decisions related to the institution of masking and social distancing mandates in communities. “Accurate epidemiological models can help policy makers choose the right course of action to help prevent further spread of infectious diseases,” Georgiou said.
Source: University of California, Irvine
10.12.2020